Articles and Books

Click to view PDF |
Title: Editorial: Radically Conventional Author: John Volan Year: 11BBz (2015d) Subject: Editorial heralding the inclusion of Pitman transdecimals in Unicode and explaining their adoption by the Bulletin. Also preludes article Base Annotation Schemes, explaining adoption of base-neutral single-character subscripts as base annotations in the Bulletin.
|

Click to view PDF |
Title: Base Annotation Schemes Author: John Volan Year: 11BBz (2015d) Subject: History of base annotations in the Dozenal Societies as well as mainstream mathematics and computing. Proposes using single-character subscripts as base-independent base annotations that do not disrupt customary prose punctuation.
|

Click to view PDF |
Title: Fundamental Operations in the Duodecimal System Author: Prof. Jay Schiffman Year: 1192z (1982d) Subject: The four basic functions, as applied in dozenal arithmetic. |

Click to view PDF |
Title: A Brief Introduction to Dozenal Counting Author: Prof. Gene Zirkel Year: 11A3z (2005d) Subject: Basics of base-twelve (dozenal) counting. |

Click to view PDF |
Title: A History of the DSA Author: Prof. Gene Zirkel Year: 11B4z (2008d) Subject: History of the Dozenal Society of America, in brief, as recounted by Prof. Gene Zirkel. |

Click to view PDF |
Title: Eggsactly a Dozen Author: Prof. James Malone Year: 1191z (1981d) Subject: An easy introduction to dozenal counting by means of the packaging of eggs. |

Click to view PDF |
Title: Decimal-Dozenal Conversion Rules Author: Prof. Gene Zirkel Year: 11B1z (2005d) Subject: Rules for converting dozenal to decimal, integers and fractions, by hand. |

Click to view PDF |
Title: Featured Figures: Basic Operations Author: Michael deVlieger Year: 11B4z (2008d) Subject: Inaugural edition of "Featured Figures": dozenal addition and multiplication tables. |
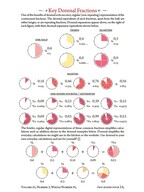
Click to view PDF |
Title: Key Dozenal Fractions Author: Michael deVlieger Year: 11B7z (2011d) Subject: Pictures and graphs illustrating dozenal's unique fractional properties. One of the reasons duodecimal is superior to decimal and any other human-scale number base is its simple representation of the commonest fractions, the half, thirds and quarters. This article includes graphs that may help elucidate this fact. |

Click to view PDF |
Title: Manual of the Dozen System (MODS) Author: Dozenal Society of America Year: 1174z (1960d) Subject: Basic introduction to dozenal mathematics; Churchman's metric system; tables. This is a classic manual which was distributed to Members and interested corresponders, which contains descriptions of various basic dozenal concepts. Tables of logarithms, exponents, and fractions are included. Also includes part of Henry Churchman’s dozenal system of measure and a section offering dozenal references. This document definitely shows its age, but still provides a useful introduction to dozenal counting and mathematics. |

Click to view PDF |
Title: Multiplication Tables of Various Bases Author: Michael deVlieger Year: 11BAz (2014d) Subject: Multiplication tables in bases 2–26z, 28z, 30z, 34z, and 50z (2–30d, 32d, 40d, and 60d). A continually-expanding set of multiplication tables for positive, integral number bases greater than 2. Makes use of Michael DeVlieger's Argam numerals for transdecimal digits. Covers bases from binary to sexagesimal (five dozen). Last updated on 11BA-0B-20z (2014-11-24d). |

Click to view PDF |
Title: The DSA’s Comprehensive Synopsis of Dozenal and Transdecimal Symbologies Author: Michael deVlieger Year: 11B7z (2011d) Subject: A poster-sized synopsis of proposals for dozenal symbologies. This 11" × 17" landscape-format poster summarizes numerals devised for dozenal, hexadecimal, and other bases. This brings together all symbols surveyed in The Duodecimal Bulletin issues Whole Number 99z (117d) and Whole Number 9Az (118d), as well as those submitted by readers and gleaned subsequently on the Internet. |

Click to view PDF |
Title: How Do You Pronounce Dozenals? Author: Prof. Gene Zirkel Year: 11B7z (2011d) Subject: The do-gro-mo system of dozenal nomenclature. Professor Zirkel gives us a new take on the do-gro-mo system of dozenal nomenclature, which was originally published in the very first issue of The Duodecimal Bulletin. |

Click to view PDF |
Title: The DozensOnline Forum Symbols Debate Author: Michael deVlieger Year: 11B6z (2010d) Subject: A debate on symbols from the DozensOnline forum. The Duodecimal Bulletin visits the DSGB’s DozensOnline web forum for a look at their discussion of numerals. |

Click to view PDF |
Title: A Numeral Toolbox Author: Michael deVlieger Year: 11B6z (2010d) Subject: Methods for devising numerals for non-decimal bases. This article, part II of a two-issue exploration of all dozenal symbologies, suggests a few simple methods of designing numerals for transdecimal number bases. Studies of “Separate Identity” symbologies reveal relationships among their numeral symbols. The symbologies of large number bases are also examined. See also Symbology Overview for Part I. |

Click to view PDF |
Title: Dozenal Mathematical Displays Using LaTeX Author: Donald P. Goodman III Year: 11B6z (2010d) Subject: A brief description of the LaTeX package "dozenal". A description of Mr. Goodman’s duodecimal extension of the LaTeX markup system, a layer of macros designed by L. Lamport which runs atop the TeX typesetting engine designed by Donald E. Knuth. |

Click to view PDF |
Title: Featured Figures: Symbology Overview Author: Michael deVlieger Year: 11B6z (2010d) Subject: This edition of Featured Figures summarizes many of the dozenal and hexadecimal numeral systems known to the DSA at the time, inspired by the DSGB’s Duodecimal Newscast articles. |

Click to view PDF |
Title: Symbology Overview Author: Michael deVlieger Year: 11B6z (2010d) Subject: Summary of least-change dozenal symbologies. The Duodecimal Bulletin examines all dozenal numeral proposals known at the time in this two-part editorial. Part I looks into “Least Change” proposals (as classified by R. Beard.) This is Part I; see also A Numeral Toolbox for Part II. |

Click to view PDF |
Title: Presenting … Symbology Author: Michael deVlieger Year: 11B6z (2010d) Subject: Introduction to the “Symbology” issue, Whole Number 99z (117d). This editorial introduces The Duodecimal Bulletin’s “Symbology Issues”, a two-issue exploration of dozenal numerals produced in 11B6z (2010d). |

Click to view PDF |
Title: The Opposed Principles Author: Ralph Beard Year: 1161z (1945d) Subject: Article originally distinguishing “least-change” and “separate-identity” symbologies. The first Editor of The Duodecimal Bulletin outlines two basic approaches to the design of numerals, the “Least-Change” and the “Separate-Identity” approaches. This article serves as the basis for the Symbology Issues of 11B6z (2010d) and the Dozenal Society of America’s policy on numerals. |

Click to view PDF |
Title: A Dozenal Nomenclature Author: Dr. Owen B. Clayton Year: 11B5z (2009d) Subject: Dr. Clayton briefly outlines his approach on how to name and symbolize dozenal numbers. |

Click to view PDF |
Title: Going Classic Author: Michael DeVlieger Year: 11B4z (2008d) Subject: Discusses the return of the Bulletin to Dwiggins numerals, away from Bell. This editorial announces return of The Duodecimal Bulletin to the “classic” Dwiggins numerals, along with a brief narrative of the use of the “Bell” numerals (* and #), and the Pitman numerals of the DSGB. |

Click to view PDF |
Title: Symbols, Symbols, !@#$%¢&*(!? Symbols Author: Prof. Gene Zirkel Year: 1192z (1982d) Subject: Explains the temporary adoption of Bell numerals by The Duodecimal Bulletin. Prof. Zirkel recounts a meeting with the DSGB’s Arthur Whillock in which dozenal numerals were discussed, and voices his espousal of the “Bell” numerals (* and #) inspired by the American telephone monopoly’s Touch-Tone keypads. The Bell numerals were used in print in The Duodecimal Bulletin between 1186z (1974d) and mid 11B4z (2008d). |

Click to view PDF |
Title: Dozenal Home Primes Author: Prof. Jay Schiffman Year: 11B7z (2011d) Subject: An explanation of dozenal home primes. Prof. Schiffman uses duodecimal to produce a set of data for each positive integer less than one gross generated by taking the digits of the integer and multiplying these together. |

Click to view PDF |
Title: On Maximal Repeating Sequence of Decimal Expansions in Base-Twelve Author: T. J. Gaffney Year: 11B6z (2010d) Subject: Exploring dozenal repeating fractions, especially sevenths. Mr. Gaffney examines the “worst case scenarios” of dozenal repeating fractional expansions, especially that associated with the sevenths. |

Click to view PDF |
Title: A Dozen Properties of the Number Twelve Author: Prof. Jay L. Schiffman Year: 1192z (1982d) Subject: Prof. Schiffman examines some number theoretical properties of the dozen. |

Click to view PDF |
Title: Music, Scales, and Dozens Author: Dr. John Impagliazzo Year: 119Az (1990d) Subject: Some different musical scales and their dozenal bases. |

Click to view PDF |
Title: Why Change? Author: Ralph Beard Year: 1164z (1948d) Subject: Why our civilization should change to dozenal. The first editor of The Duodecimal Bulletin likens the duodecimal number base with the adoption of Hindu-Arabic numerals and positional notation in medieval Europe, which took centuries replace the old Roman numerals. Dozenal must eventually replace decimal, because decimal has “not enough factors” when compared to dozenal. |

Click to view PDF |
Title: Twelves and Tens? Author: A. C. Aitken Year: 1164z (1965d) Subject: Why dozenal is superior to decimal. Mr. Aitken writes in The Listener makes a case for dozenal, citing fractions and the revolutionary ardor of French promoters of the decimal metric system. |

Click to view PDF |
Title: An Excursion in Numbers Author: F. Emerson Andrews Year: 1152z (1934d) Subject: Why dozens are a better base than decimal. The landmark article in the Atlantic Monthly, which eventually led to the founding of the Duodecimal Society of America. |

Click to view PDF |
Title: My Love Affair with Dozens Author: F. Emerson Andrews Year: 1184z (1972d) Subject: How Andrews fell in love with dozenal. One of the DSA’s Founders describes how he, a writer, fell in love with the number twelve through reason, and how the Duodecimal Society of America came to be established. |

Click to view PDF |
Title: Reflections on the DSGB Author: Prof. Gene Zirkel Year: 11B5z (2009d) Subject: Some reflections on the Dozenal Society of Great Britain. Prof. Zirkel compiled some thoughts from key DSGB Members including Brian Bishop, Shaun Ferguson, and Robert Carnaghan on the history of the Dozenal Society of Great Britain. Part II of two. |

Click to view PDF |
Title: DSA Constitution and Bylaws Author: Dozenal Society of America Year: 1197z (1987d) Subject: The current Constitution and Bylaws of the DSA. |

Click to view PDF |
Title: Dozenal FAQ Author: Michael deVlieger Year: 11B7z (2011d) Subject: A comprehensive explanation of the benefits of the dozenal base. Answers to a dozen frequently asked questions about dozenal, fully illustrated. Two dozen pages explaining why duodecimal is the optimum number base for general human intuitive computation. Answers include benefits of dozenal beyond the often-heard reasons of the large number of divisors and “easy fractions”. Candid responses describing the drawbacks of dozenal and the benefits of decimal. |

Click to view PDF |
Title: Some Notes on the History and Desirability of Using Alternate Number Bases in Arithmetic Author: Christopher J. Osburn Year: 11B5z (2009d) Subject: Comparison study of several alternate bases. Mr. Osburn’s article examines the number theoretical properties of the dozen and other bases, concluding that twelve would be the optimum base for computation. |

Click to view PDF |
Title: Analysis of Multiplication Tables Author: Michael deVlieger Year: 11B7z (2011d) Subject: Comparing the traits of the multiplication tables of various bases. The optimum number base may be more or less attributable to a number’s prime factorization. The behavior of a number base’s digits, from periodicity in the multiplication table to regularity in fractions, is governed by the number-theoretical relationships of each digit to the base. |

Click to view PDF |
Title: Antipatio al Aritmetiko Author: Ralph Beard Year: 1171z (1957d) Subject: Ralph Beard makes the case for dozenalism, in Esperanto. The DSA's initial outreach to the Esperanto community: a translation of Ralph Beard’s article “Aversion to Arithmetic” into Esperanto |

Click to view PDF |
Title: The Aspirant’s Tests Author: Dozenal Society of America Year: circa 1161z (1945d) Subject: Tests for proficiency in the dozenal system. Remastered versions of all four of the old DSA aspirant’s tests, passage of which was formerly required for membership in the Society. Answers are included, with convenient links from each question to its answer. |

Click to view PDF |
Title: TGM: A Coherent Dozenal Metrology Author: Tom Pendlebury / Donald P. Goodman III Year: 11E8z (2012d) Subject: Description of the TGM complete dozenal system of weights and measures. NOTE: This book is now available in print for only $8. This is nearly at cost. All profits will be donated to the DSA. This book gives a complete picture of the TGM (Tim, Grafut, Maz) dozenal system of weights and measures. It is a complete system, covering all fields of scientific endeavor, and is consistently dozenal. It also maintains a 1 : 1 correspondence between basic measures. TGM was designed by Tom Pendlebury of the Dozenal Society of Great Britain over the course of many years. This updated description of the system was prepared by Donald P. Goodman of the DSA, with heavy reliance on Mr. Pendlebury’s original work. The book uses Systematic Dozenal Nomenclature for referring to dozenal numbers. This edition includes:
Note that this is not a publication of the Dozenal Society of America, which does not endorse any particular proposal for a dozenal system of measures. It is offered here simply because of its interest and importance to the dozenal community. A great deal of further information about TGM can be found at Dozenalism’s TGM. |

Click to view PDF |
Title: Boxes & Cans: Some Points on Packaging Author: Donald Hammond (“Troy”) Year: 1193z (1983d) Subject: Dozenal’s advantages in packaging. Originally published in the old joint journal of the Dozenal Society of Great Britain and the Dozenal Society of America, The Dozenal Journal, this wonderful article explores the basics of packaging and shows that dozenal has the greatest advantage. Carefully and simply explaining the principles of packaging, and separating the more technical math from the basic, the DSGB’s “Troy” clearly demonstrates dozenal’s advantages in this field. In fact, “Troy” is able to prove that a twelve-pack is so much more efficient than a ten-pack that packing ten cans in a twelve-pack, leaving two empty spaces, is actually cheaper than packing ten in a ten-pack! The DSA is pleased to be able to present this remastered version this article. Originally published in two parts, it is here presented as a whole. |

Click to view PDF |
Author: Thomas Leech, F.C.S. Year: 10B6z (1866d) Subject: Defense of dozenal notation for arithmetic, weights, measures, and money. Originally published in 10B6z (1866d), this is quite probably the first modern-era, serious, and full-length exposition of the dozenal system ever written. At over 100z (144d) years old, it’s remarkable how well this work withstands the test of time. Many of the Leech’s practical suggestions aren’t really applicable to our time. However, as a discussion of dozenal remarkable in its completeness, it is still an interesting read. |

Click to view PDF |
Title: Dozenal Divisibility Tests Quick Guide Author: Treisaran Year: 11B9z (2013d) Subject: Dozenal divisibility tests An invaluable resource for anyone who wants to become more adept with dozenal arithmetic, particularly mental arithmetic. This fact sheet puts together all the major divisibility tests of the dozenal system into a single, easy-to-learn and easy-to-understand package. |

Click to view PDF |
Title: Systems of Numeration: A Plea for the Duodecimal Author: Rev. Thomas J. A. Freeman, S.J. Year: 1119z (1893d) Subject: An early plea for the adoption of the dozenal base. Inspired by an earlier work by William B. Smith, this is a delightfully light-hearted, yet thorough, introduction to bases and to dozenal (which Rev. Freeman calls duodecimal or telimal throughout). Rarely for a mathematical article, this one even includes jokes and poetry. A very early work on the topic, this article takes the reader through the basic concepts of base notation, to why dozenal is the superior base, to metric systems, and to systems of nomenclature. An excellent addition to any dozenal reading-list. |

Click to view PDF |
Title: The Number Rhyme Author: Donald P. Goodman III Year: 11B9z (2013d) Subject: A simple rhyme teaching counting and the basic characteristics of number one to a dozen. A simple rhyme describing the basic characteristics of the numbers 1–10z (one through a dozen), intended to be useful for students, particularly young children. More advanced that the traditional “One, two, buckle my shoe,” but designed to be a similar way to teach counting, though this rhyme at the same time teaches something about the numbers themselves. |

Click to view PDF |
Title: RAENBO Dozenals Author: Timothy Travis Year: 11B9z (2013d) Subject: Travis’ RAENBO system of dozenals. In this document, DSA board member Timothy Travis (member 342z) presents some beautiful graphics and commentary regarding his love for dozenals and his ideas for using them. The playing-card back he designed is especially lovely. |

Click to view PDF |
Title: Duodenal System of Arithmetic, Measures, Weights and Coins Author: John William Nystrom Year: 1103z (1875d) Subject: A defense of dozenal arithmetic and measurement, along with proposed symbols, nomenclature, and metrics. John William Nystrom, a famous Swedish-American engineer, 1081–1111z (1825–1885d), is mostly known mathematically for his unquadral (hexadecimal) “Tonal” system. However, later in life, Nystrom became a dozenalist, publishing the current article as an appendix to a textbook on mechanics. The DSA is proud to offer this remastered version of Nystrom’s arrival at dozenalism, noting that it contains a great deal of food for thought for anyone interesting in number bases. |

Click to view PDF |
Title: Laplace sur Douzainisme Author: Pierre-Simon Laplace Year: 109Az (1846d) Subject: La systeme de la douzaine (la systeme duodecimale) en bref. Dans ce morceau, M. Laplace admets la supériorité de la système de la douzaine (la système duodécimale), parce que douze est divisible par trois et par quatre, mais il croit que les deux tableaux additionnels (pour dix et onze) sont trop difficiles pour le petits esprits du peuple. Le fils du paysan, on pense, doit avoir une meilleure opinion du abilité mathématique du peuple, qui souvent sait ces tableaux même dans la système décimale. Mais néanmoins, ce grand mathématicien clairement a pensé que la système de la douzaine est meilleure que décimale, un grand endossement vraiment. |

Click to view PDF |
Title: Leclerc sur Douzainisme Author: Georges-Louise Leclerc, Comte de Buffon Year: 1041z (1777d) Subject: Une morceau de Georges-Louis Leclerc, Comte de Buffon, d’avantage de la douzaine dans arithmetique. |

Click to view PDF |
Title: Playfair on Dozenalism Author: John Playfair Year: 1067z (1807d) Subject: An early English defense of the dozenal system. John Playfair, in his comments on the French Revolution, notes that it found itself in the unique position of being able to cast off all the shackles of a past age, yet was still too timid to cast off the most obvious mathematical shackle of all: the decimal system. An early defense of dozenalism, conducted not long after the French Revolution as an aside in some comments on the definition of the meter. |

Click to view PDF |
Title: Systematic Dozenal Nomenclature Author: John Volan (“Kodegadulo”) Year: 11BAz (2014d) Subject: Systematic Dozenal Nomenclature. Sytematic Dozenal Nomenclature is a powerful and robust way of speaking about and using dozenal numbers that was developed during a discussion thread on the DozensOnline forum that was lead by John Volan (“Kodegadulo”) in 11B7z (2011d). SDN is a classically-grounded set of technical prefixes based on an extension of the digit roots used for Systematic Element Names, as well as the Latin word uncia. It acts as a replacement for TGM’s power prefixes, avoiding their oddness while embodying the same underlying principles. This is the fully-fleshed out, definitive work on SDN. Described in several parts in the DSA’s Newscast in 11B9z (2013d), the system was summarized in an article by Donald Goodman III in The Duodecimal Bulletin Whole Number A0z (120d), followed by the full exposition in this article, originally published in The Duodecimal Bulletin Whole Number A1z (121d). This standalone version was produced from a revised source provided by the author. |

Click to view PDF |
Title: Twelve vs. Ten Author: William B. Smith Year: 1117z (1891d) Subject: A brief, turn-of-the-century defense of the dozenal base. Written in a stern and scholarly late-nineteenth-century style, William B. Smith, in an article which inspired the much more accessible piece by Rev. Thomas Freeman, this article sets out the case for conversion to a dozenal base. It makes a brief but compelling case for the superiority of dozenal over decimal, sets out a system of dozenal nomenclature, uses "t" and "e" (like Freeman) for "ten" and "eleven," and even outlines a system of metrology based on the hour and the yard. |

Click to view PDF |
Title: A Rational Solution to the Problem of Weights and Measures Author: Sidney A. Reeve Year: 1127z (1903d) Subject:A defense of the dozenal system from the perspective of a mechanical engineer. |

Click to view PDF |
Title: A Duodecimal Scale Author: Dr. Edward Brooks Year: 1104z (1876d) Subject: A late Nineteenth-Century (early Dozen-Second-Biquennium) account of dozenal arithmetic and notation. This work by Dr. Edward Brooks, a famed philosopher of mathematics, explains his system of dozenal notation and gives a brief explanation of arithmetic in dozenal, providing examples of all four functions. Yet another excellent piece from a distinguished mathematician showing the benefits of the dozenal system. |

Click to view PDF |
Title: Filosofia de la numeración Author: D. Vicente Pujals de la Bastida Year: 1098z (1844d) Subject: La superioridad de la doce como un base de la numeración. Un libro en español sobre la superioridad de la doce como un base de la numeración. |

Click to view PDF |
Title: De la numeración que debe preferirse Author: D. Vicente Pujals de la Bastida Year: 1098z (1844d) Subject: Cuya base debe elegir? Un extracto de Filosofia de la numeracion por D. Vicente Pujals de la Bastida. |

Click to view PDF |
Title: De Arithmetica quae per Periodos Duodenarias Recurreret Author: Ioannis Caramuelis (Juan Caramuel y Lobkowitz) Year: B48z (1640d) Subject: Very early exposition of dozenal, written in Latin In a time in which “astronomy” and “mathematics” were nearly synonymous among Europe’s educated elite, Ioannis Caramuelis, known more commonly by his Spanish name Juan Caramuel y Lobkowitz, penned this brief but brilliant defense of dozenal in the universal language of the time, Latin. The earliest discussion of dozenal yet known, Lobkowitz uses “p” for ten (the digits “1” and “0” combined) and “n” for eleven (two digit “1”s connected by a swash at the top). He explains and demonstrates the four arithmetic functions, including both a “basic” and “advanced” division (corresponding to our “short” and “long" division), and urges the adoption of the dozenal system in astronomy. A brilliant work, very much ahead of its time; provided here in its original Latin, with parallel English translation. |

Click to view PDF |
Title: Rationality Author: Donald Hammond (“Troy”) Year: 11A0z (1992d) Subject: The role of ratios in weights and measures. Written by long-time DSGB pillar Donald Hammond under the exceedingly apt pseudonym “Troy,” this work expounds on the notion of “rationality” in arithmetic and weight and measures. Explaining that “rationality” means taking into account the appropriate ratios, Hammond explains how the “troy” system (dozenal) is more efficient in most applications than decimal, and proposes an interestingly different version of the protractor. The discussion of kitchen weights and bricklaying are particularly interesting. |

Click to view PDF |
Title: The Duodecimal System of Notation Author: L. H. Vincent Year: 1131z (1909d) Subject: A simple, mostly verbal argument for dozenal. This article by L. H. Vincent gives a refreshingly simple, yet compelling case for base twelve. Word-heavy and math-light, he lays out the dozenal system with only one small table and no embedded mathematics. |

Click to view PDF |
Title: Collected Works on Reckoning Reform Author: Sir Isaac Pitman Year: 10A8z (1856d) Subject:Collected works of Sir Isaac Pitman on the dozenal base. Sir Isaac Pitman was one of the earlier consistent proponents of a dozenal system, and this article presents four pieces in which he proposed and defended the system. Better known for his system of shorthand, his work on the “reckoning reform” deserves more attention. One of these works, titled “Reckoning Reform,” marks one of the first uses of the now-common “Pitman” characters for ten and eleven, which as of 11BBz (2015d) have been included in the Unicode standard. |

Click to view PDF |
Title: Practical Polygons Author: Donald Hammond (“Troy”) Year: 1196z (1986d) Subject:Numbers considered through polygons. This powerful article discusses numbers in the form of two-dimensional plane figures, explaining how polygons show the nature of number and demonstrate the superiority of twelve as a counting base. Richly i llustrated and explained. |

Click to view PDF |
Title: Mathamerica Author: Grover Cleveland Perry Year: 1149z (1929d) Subject: A stridently patriotic argument in favor of dozenals from an interwar Protestant American viewpoint. Written during the period between the two World Wars, Mathamerica is almost more of a paean to the semi-imperialist Protestant American views of its author than to dozenals. However, despite its jingoism and provincialism, the work does contain much that could be interesting to dozenalists, particularly students of the history of dozenal and other non-decimal bases. Written in the years preceding our own F. Emerson Andrews’s more broadly-based work, Grover Cleveland Perry’s pamphlet Mathamerica reviews dozens, fractions, basic arithmetic, and basic geometry in his justification for and praise of dozenals. An interesting addition to the Dozenal Society of America’s library. |

Click to view PDF |
Title: Against the Metric System Author: Herbert Spencer Year: 1122z (1898d) Subject: A critique of the metric system (and the customary-imperial system) and a defense of dozenals. Written by Herbert Spencer during one of the earlier pushes toward the metric system in Britain, this piece attacks the metric system on a number of grounds. However, it does not defend the customary-imperial system; far from it. It identifies the major problem with both systems as their being decimal, and explains the superiority of dozenal arithmetic. |

Click to view PDF |
Title: La Zonnomie, ou La Décimale et la Duodécimale Author: A.-D. Gautier Year: 10B0z (1860d) Subject: Un explication de la système de douzainisme, avec des nouveaux chiffres et un système de mesure et d’argent. Ce petit livre explique brièvement les avantages et les méthodes de faire des mathématiques par la douzaine. Il fournit un système complet de nouveaux chiffres, de mesures et d’argent. Certainement, beaucoup de ses idées n'aient pas été adoptées par la communauté de la douzainisme, c’est encore une grande démonstration de la vaste gamme de douzaine d’écrivains, et une grande explication de la système de douzaine en général. |

Click to view PDF |
Title: Manual of the Dozenal System (Revised) Author: Donald P. Goodman III Year: 1200z (2016d) Subject: A short but thorough introduction to dozenals for those really interested in learning and using them. Clocking in at four dozen pages, this work is the updated version of the original Manual of the Dozen System published in 1174z (1960d). Fully updated for the digital world, this document is a great handbook for those wishing to learn and really use dozens. Available for sale at Lulu.
|

Click to view PDF |
Title: A Dozenal Primer Author: Donald P. Goodman III Year: 1200z (2016d) Subject: A brief explanation of the dozenal system designed for beginners, in only a dozen pages. This little book is designed as a quick and easy introduction to dozenal for those who have no interest or knowledge of them. Weighing in at only a dozen pages, it is an ideal way to display the advantages of dozenal without overwhelming the non-mathematically-inclined. Available for sale at Lulu. |

Click to view PDF |
Title: The Duodenary Scale Author: John Wilkes, Ed. Year: 1078z (1820d) Subject: An exploration of dozenal arithmetic and its advantages. A brief explanation and demonstration of dozenal arithmetic, originally published as part of Wilkes’ Encyclopaedia Londinensis. Reproduced verbatim (with the sole exception of replacing the archaic “long s” with our normal “s”), this provides an interesting, and short, glimpse at the dozenal considerations of its time. |

Click to view PDF |
Title: The Personality of the Integers from One to One Gross Author: Prof. Jay Schiffman Year: 11A3z (1995d) Subject: A scholarly, if brief, exploration of the major properties of the integers between 1 and 100z (144d). A brief but scholarly exploration of the major properties of the integers from 1 to 100z (144d), and how those properties give an integer its particular “personality.” Original printed in The Duodecimal Bulletin, Whole Number 74z (88d), this article has been newly typeset and corrected. Reviews a few major integer sequences; divisors; and other important properties. |

Click to view PDF |
Title: Is the decimal system appropriate for modern mathematics? Author: Naomi Wray Year: 1202z (2018d) Subject: Ms. Wray gives an excellent examination of the decimal base and its suitability for modern mathematics. Naomi Wray, in an extended project qualification from 1201/1202z (2017/2018d), has written a brief but excellent examination of number bases in modern mathematics. Attractively designed and well-composed, the article examines the rise of decimal and its disadvantages, along with the advantages of the dozenal base. It relies in several places on our DSA publications (even citing a dozenal limerick from the DSA Newscast 3:10!). An entertaining and enlightening read. |

Click to view PDF |
Title: De Numeratione Author: Brian Bishop (“Brennus Legranus”) Year: 1203z (2019d) Subject: An erudite and stimulating article concerning the basis and nature of dozenal. In the original Latin. Longtime DSGB stalwart and passionate classicist Brian Bishop (a.k.a “Brennus Legranus”) writes a beautiful, elegant, and informative introduction to dozenals in Latin. Classicists everywhere will delight in his style and diction, and will learn something about dozenals, too. |

Click to view PDF |
Title: An Ancient Duodecimal System Author: Rufus P. Williams Year: 1131z (1909d) Subject: A brief look at the “pure” ancient duodecimal system of measures, primarily in the relation between the foot, pint, and bushel. Rufus P. Williams, writing in 1131z (1909d) in the journal School Science and Mathematics, hypothesizes a “pure” dozenal system of weights and measures, with a foot for length; a bushel for weight; and a pint for volume, and the superiority of this system over decimal alternatives. While he’s very pessimistic about the potential success of dozenals at all, he does make some excellent observations about twelve as the ideal basis for a system of measures. |

Click to view PDF |
Title: Trigons to Triads: A Play on Chords Author: Donald Hammond (“Troy”) Year: 119Bz (1991d) Subject: An exploration of triangles, Pythagrean triples, and their unique relationship to dozens “Troy” (Donald Hammond, of the DSGB) writes a fascinating little article about triangles; Pythagorean triples; and how they relate to chords, and provides a wonderful little printable “chord dialer” that uses the innate properties of the dozen to identify harmonious chords for music. |




